Randomisierung verstehen
Randomisierung - Was ist das?
Unter Randomisierung versteht man in der klinischen Forschung die zufällige Zuteilung von Studien-Teilnehmern (z.B. Patienten) zu den verschiedenen Therapiegruppen der Studie.
Das hört sich erst mal einfach an, kann aber beliebig kompliziert durchgeführt werden.
Randomisierung ist häufig eine essentielle Anforderung, ohne deren Erfüllung die Ergebnisse der Studie nicht anerkannt werden.
Warum das so ist und welche Randomisierungs-Verfahren es gibt, wird in den folgenden Abschnitten beschrieben.
Randomisierung in klinischen Studien - Warum?
Der bestmögliche Studientyp, also der “Goldstandard” bei der Wahl eines Studiendesigns, ist die randomisierte kontrollierte klinische Studie (engl. RCT: randomized controlled trial). Seit 1949 wird sie in der klinischen Forschung eingesetzt. Wesentliches Qualitätsmerkmal dieses Studientyps ist die Randomisierung, also die zufällige Zuteilung der Patienten auf die untersuchten Behandlungsgruppen. Dies ist die einzige Methode, Effekte von Störgrößen auszuschalten, die unbekannt sind oder nicht durch Blockbildung beziehungsweise Stratifizierung eliminiert werden können.
Um FDA und ICH GCP Richtlinien zu erfüllen, muss die Randomisierung computergestützt erfolgen. Beispielsweise weil zur Veröffentlichung nachvollziehbarer und reproduzierbarer wissenschaftlicher Ergebnisse auch gehört, dass der komplette Randomisierungsprozess richtlinienkonform und dokumentiert durchgeführt wird.
Besonders flexibel einsetzbar sind Randomisierungsprogramme dann, wenn Sie eine serviceorientierte Architektur haben und z.B. über eine Webseite angesprochen werden können. Erst dadurch wird beispielsweise eine adaptive multizentrische Echtzeitrandomisierung mit vertretbarem Aufwand möglich.
Motivation
“...[Es] soll mit einer Patientengruppe ein Aufmerksamkeitstraining durchgeführt werden und mit der anderen Gruppe ein unspezifisches Hirnleistungstraining verschiedener kognitiver Funktionen. Die Klinik meint, wenn ich 32 Lose in eine Kiste gebe (jeweils 16 für die eine und 16 für die andere Gruppe) und ohne Zurücklegen für jeden neuen, an der Studie teilnehmenden Patienten ein Los ziehe, dann genüge das als Randomisierung.”, Psychologiestudentin, Ende 2009.
Genügt das den Anforderungen einer wissenschaftlichen, klinischen Studie?
- Nein, denn der Vorgang ist nicht reproduzierbar! Die Studentin könnte z.B. absichtlich oder unabsichtlich bestimmte Patienten bevorzugt in eine bestimmte Gruppe zuteilen.
So einfach die oben beschriebene Randomisierung auch ist, es handelt sich bereits um ein spezielles Randomisierungsdesign:
PBR, 2 Gruppen, B = 32
Nachteil: Vorhersagbarkeit. Angenommen die ersten 16 Patienten kommen zufällig alle in Gruppe 1, dann kommen die verbleibenden Patienten automatisch in Gruppe 2!
Warum computergestützt Randomisieren und nicht Lose ziehen?
Design I: Auswahl des richtigen Randomisierungsverfahrens
Gütekriterien
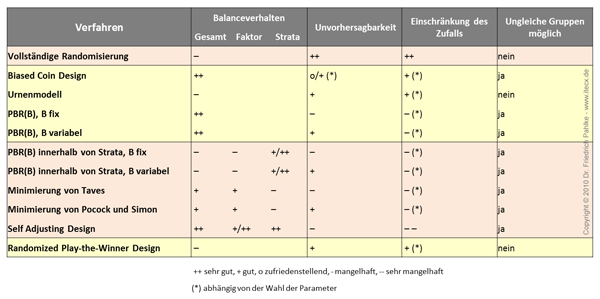
Wie bewertet man die verschiedenen Verfahren?
Wie gut ist das Balanceverhalten (Gesamt, Faktor, Stratum)
Unvorhersagbarkeit: Kann der Arzt das Randomisierungsverfahren raten, da es eine Systematik erkennen lässt?
Grad der Zufallseinschränkung: Wie stark wird der Zufall eingeschränkt, um die Balance zu verbessern?
Welche Randomisierungsverfahren gibt es?
Vollständige Randomisierung (Complete)
Basisadaptive Verfahren (Baseline-adaptive)
BCD – Biased Coin Design (Efron 1971)
URN – Urnen Modell (Wei 1978)
PBR – Permutierte Blockrandomisierung (Zelen 1974)
Kovariaten-adaptive Verfahren (Covariate-adaptive)
PBR Strata – Permutierte Blockrandomisierung innerhalb von Strata (Zelen 1974)
Minimierung (Taves 1974)
Minimierung (Pocock und Simon 1975)
Self-Adjusting Design (Nordle und Brantmark 1977)
Responseadaptive Verfahren (Response-adaptive)
RPW – Randomized Play-the-Winner Design (Wei und Durham 1978)
Kovariaten-adjustierte response-adaptive Verfahren (Covariate-adjusted response-adaptive)
Modellbasierte Verfahren
Entscheidungsbaum
Welches Verfahren ist für mich das Beste? Bevor das Verfahren bezüglich der genannten Gütekriterien überprüft werden kann, muss im ersten Schritt die Design-Gruppe (Klasse) ermittelt werden:
Im zweiten Schritte können dann die einzelnen Verfahren bezüglich der genannten Gütekriterien überprüft werden:
Design II: Auswahl der Randomisierungsparameter
Es gibt eine Vielzahl verschiedener Randomisierungsparameter, beispielsweise
BCD: p,
URN: w, α, β,
PBR: B,
Minimierung (Pocock & Simon): p,
RPW: w, α, β.
Die Auswahl von Parameterwerten, die zum individuellen Studiendesign passen, stellt häufig ein Problem dar, das nicht pauschal, sondern nur in Abhängigkeit der spezifischen Studienvorgaben gelöst werden kann. So gibt es zwar eine Reihe von Standardwerten für die verschiedenen Randomisierungsverfahren, für zwei Therapiegruppen werden z.B. häufig folgende Werte gewählt:
BCD: p = 2/3,
URN: w = 1, α = 1, β = 2 (β ≥ α),
PBR: B = 4 oder 8 (variabel),
Minimierung (Pocock & Simon): p = 0.85,
RPW: w = 1, α = 1, β = 1 (α = Erfolg, β = Misserfolg).
Bei drei Therapiegruppen ist die Auswahl dagegen schon deutlich komplizierter und es fehlt an Empfehlungen.
Beispiel BCD: Wie sollen die Parameter gewählt werden?
p1 = 0.5, p2 = 0.3, p3 = 0.2 oder
p1 = 0.6, p2 = 0.2, p3 = 0.2?
Beispiel PBR: Wie sollen die Parameter gewählt werden?
B = 6 oder 9 (variabel) oder
B = 30?
Die Parameterwahl kann durch weitere Faktoren erschwert werden, beispielsweise wenn Therapiegruppen ungleicher Größe erreicht werden sollen. Das kann z.B. aus ethischen Gründen sinnvoll sein: Eine gute Therapie sollte u.U. bevorzugt werden (vgl. RPW). Oder: Die Anforderungen von Tierstudien haben in der Praxis häufig kleine Fallzahlen mit sehr speziell besetzten ungleichen Gruppen.
Ein wichtiges Hilfsmittel bei der Wahl geeigneter Parameterwerte können Simulationen darstellen, mit deren Hilfe verschiedene mögliche Parameterkonstellationen im gegebenen Studien-Setting simuliert werden.
Informationstechnische Herausforderungen
Bei der Implementierung der Algorithmen gilt es verschiedene Herausforderungen zu meistern. Dazu gehören beispielsweise
Die Generierung von guten Zufallszahlen:
Es können entweder Pseudozufallszahlen per Algorithmus erzeugt werden. Vorteil: Eine Reproduktion aller Zahlen ist mit Hilfe eines einzigen Startwertes, dem sogenannten Seed, möglich.
Oder es können echte Zufallszahlen benutzt werden, z.B. auf Basis von Atomzerfall oder weißem Rauschen.
Numerische Probleme:
Genauigkeit: 32 oder 64 Bit
Rundungsunterschiede
Beispiel: geg. Zufallszahl r = 0.49999...97
T1, falls 0 ≤ r < 0.5
T2, falls 0.5 ≤ r ≤ 1
Je nachdem ob und wie gerundet wird, kommt der Patient in Gruppe 1 oder Gruppe 2
Der Server muss bestimmten Anforderungen genügen, z.B.
Eine Sichere Verblindung ist zu gewährleisten,
außerdem die Hochverfügbarkeit 24 Stunden, 7 Tage die Woche,
Regelmäßige Datensicherungen sind durchzuführen,
die Daten-Redundanz über große physikalische Distanz (mindesten 100 km) ist empfehlenswert.