Korrelationskoeffizienten interpretieren
Frage
Wie interpretiere ich eine Korrelationsmatrix bzw. einen Korrelationskoeffizienten? Welche Werte können Korrelationskoeffizienten annehmen?
Antwort
Falls die Korrelationsmatrix noch nicht als Excel-Datei vorliegt, sollte diese zunächst als Excel-Datei exportiert werden.
Eine typische Korrelationsmatrix mit 10 Merkmalen sieht wie folgt aus:
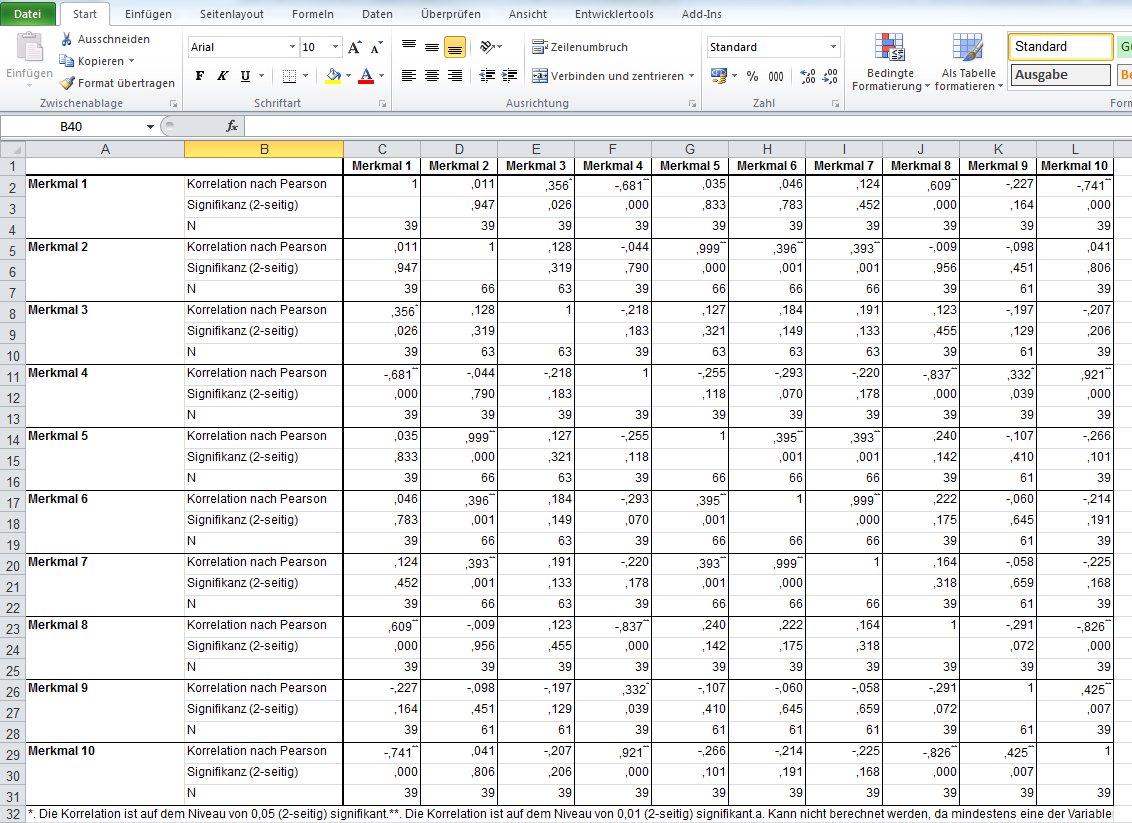
Es bietet sich an, zunächst alle signifikanten Korrelationskoeffizienten farblich hervorzuheben.
Eine detaillierte Anleitung dafür findest Du hier: Korrelationskoeffizienten mit Excel farblich hervorheben.
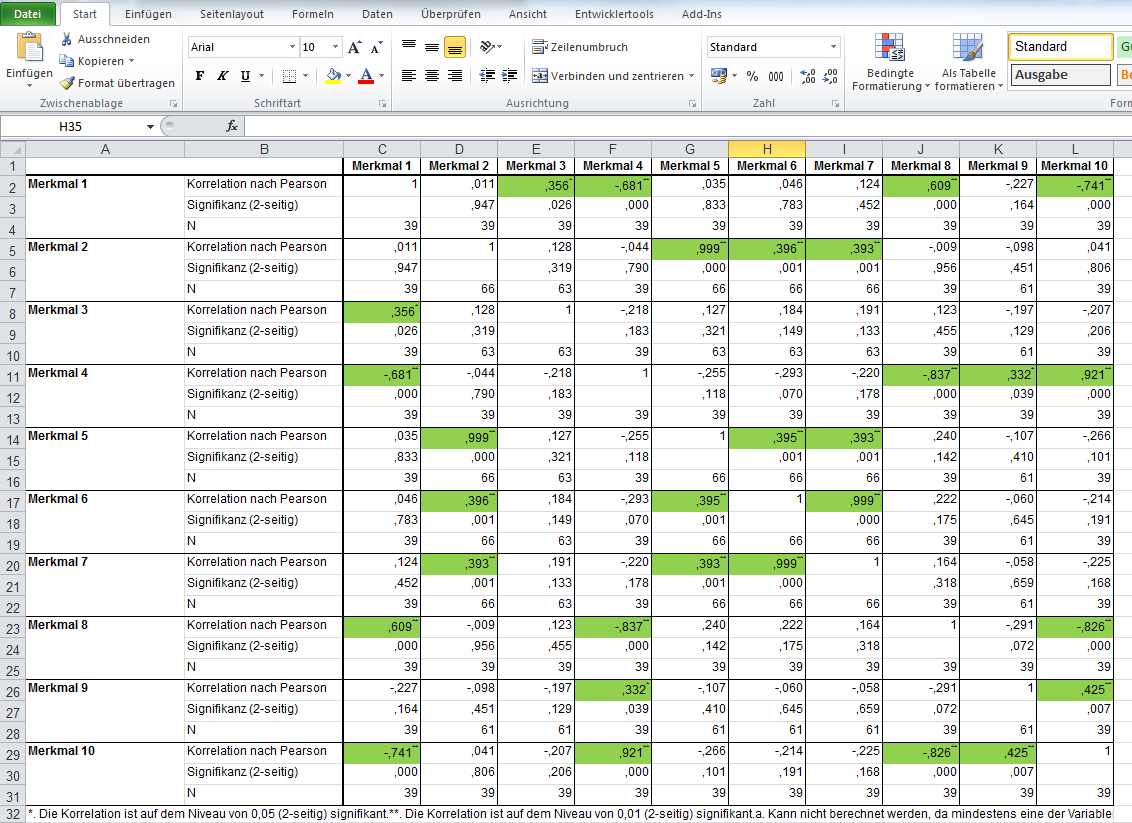
Unter jedem Korrelationskoeffizienten in der Tabelle steht ein p-Wert, der anzeigt, ob der Korrelationskoeffizient darüber signifikant von Null verschieden ist, d.h. ob die Abweichung des ermittelten Korrelationskoeffizienten von Null auch signifikant ist. Nur wenn dieser p-Wert = 0.05 ist, darf man von einem statistischen Zusammenhang zwischen den betrachteten Merkmalen (Variablen) sprechen.
Wichtig: Dieser p-Wert zeigt nicht, ob es einen signifikanten Unterschied zwischen den beiden betrachteten Merkmalen gibt!

Alle grün hinterlegten Korrelationskoeffizienten, d.h. Korrelationskoeffizienten mit einem * oder ** (siehe Fußnote unter der Tabelle), zeigen die Stärke des Zusammenhangs zwischen dem Merkmalen in derselben Zeile und Spalte.
Beispielsweise ist Merkmal 4 signifikant negativ mit Merkmal 1 korreliert (r = -0,681). Anders ausgesprochen: Es gibt einen mittelstarken negativen Zusammenhang zwischen Merkmal 4 und Merkmal 1, d.h. umso höher die Werte von Merkmal 4, umso niedriger sind die Werte von Merkmal
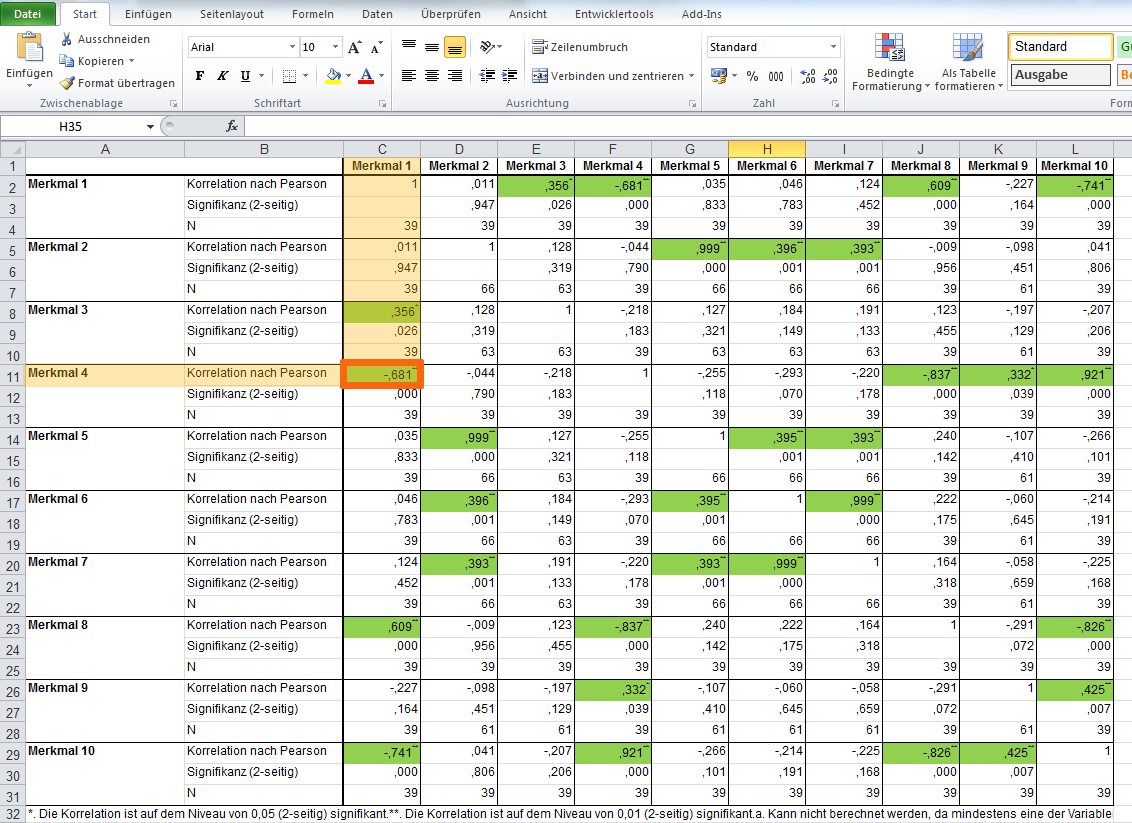
Wertebereich von Korrelationskoeffizienten
- Kann Werte zwischen -1 und +1 annehmen
- Wert +1 = vollständig positiver linearer Zusammenhang zwischen den betrachteten Merkmalen
- Wert -1 = vollständig negativer linearer Zusammenhang
- Wert 0 = die beiden Merkmale hängen überhaupt nicht linear voneinander ab
Faustregeln für die Interpretation von Korrelationskoeffizienten
- 0 = kein linearer Zusammenhang
- 0,3 = schwach positiver linearer Zusammenhang
- 0,5 = mittelstarker positiver linearer Zusammenhang
- 0,8 = starker positiver linearer Zusammenhang
- -0,3 = schwach negativer linearer Zusammenhang
- -0,5 = mittelstarker negativer linearer Zusammenhang
- -0,8 = starker negativer linearer Zusammenhang
Welchen Korrelationskoeffizienten soll ich nehmen?
Der Pearsonsche Korrelationskoeffizient k ist geeignet bei intervallskalierten (z.B. Körpergewicht in Kg) und bei dichotomen Daten (z.B. Geschlecht m/w). Intervallskalierte Variablen müssen annähernd normalverteilt sein.
Ist das nicht der Fall, sollte einer der beiden Rangkorrelationskoeffizienten Kendals Tau oder Spearmans Roh benutzt werden.
Beispiel: Aus den Daten geht hervor, dass Variable A die Werte “0 = no” und “1 = yes” annehmen kann. Falls der Korrelationskoeffizient einen positiven Zusammenhang zu Variable B nahelegt, dann bedeutet das: Wenn A = no, dann sind die Werte von B kleiner, wenn A = yes, dann sind die Werte von B größer.